Threshold signatures

Reference

Overview

This page gives a high-level outline of threshold signatures on ICP. Some of the information in this section is not required to use threshold signing features, but may be of interest to the technically inclined reader for obtaining background information on the technology. ICP currently supports threshold Schnorr signing and threshold ECDSA signing. Further research on ECDSA is described by Groth and Shoup in their Eurocrypt 2022 paper. Groth and Shoup have also published a comprehensive design and analysis of ECDSA. For Schnorr, various designs were propsed by Groth and Shoup and a security analysis of Schnorr from Shoup was completed.

At a high level, the threshold signature implementations on ICP feature multiple protocols as outlined next, all of which are crucial for a secure system setup and operation. Note that this goes far beyond just threshold signing, which is the reason for calling this a protocol suite for chain-key signatures.

• Key generation: this protocol is executed on a specified subnet; it generates a new threshold key such that the private key is secret shared over the replicas of this subnet.
• XNet key re-sharing: this protocol re-shares a key from a source subnet to a target subnet. It results in the same key being secret shared over the replicas of the target subnet using a different random secret sharing (potentially over a different number of replicas than the sharing in the source subnet uses).
• Periodic key re-sharing: this protocol re-shares a key within the subnet it is secret shared on. This helps protect against an adaptive attacker that attempts to compromise replicas over time as every key resharing makes the previously-obtained key shares worthless.
• Computing pre-signatures, signing: these protocols compute signatures with the secret-shared private key. A protocol for computing pre signatures that is run asynchronously to the signing protocol, and it is often run before a signature is requested. This precomputation protocol computes the vast majority of the steps of creating threshold signatures. A signing protocol is triggered by a signing request of a canister. A signing protocol consumes one pre-signature to efficiently compute a threshold signature.
• Public key retrieval: allows for retrieving a public key of a canister, including potential BIP-32-like key derivation based on a canister-provided derivation path.

It is crucial to note that the private key never exists in a reconstructed form, and only in secret-shared form during its whole lifetime, whether that is the key's generation, the re-sharing of the key within a subnet or from one subnet to another, or when computing signatures.

Various NNS proposals have been implemented to perform key management, i.e., initial key generation and key re-sharing. Those proposals are used to define on which subnet to generate a master key, to which subnet to re-share the key for better availability, and which subnet to enable for answering signing requests.

Threshold keys

Threshold-signature (t-sig) enabled subnets hold what are called threshold master keys, generated with the key generation protocol on selected subnets of ICP. A master key is a key from which canister t-sig keys can be derived, i.e., a single master key for a given elliptic curve suffices for the derivation of a t-sig key for each canister on ICP, the canister root key, using an extension of the BIP-32 key derivation mechanism with the canister's principal as input. Key derivation is executed transparently by the protocol as part of the signing and public key retrieval APIs. See the level-0 key derivation in the below figure for the derivation of canister root keys from a master key.

From a canister root key, an unlimited number of t-sig keys can be derived for the canister using a backward-compatible extension of the BIP-32 key derivation mechanism. The extension allows not only 32-bit integers, but arbitrary-length byte arrays, to be used as input for each level of the key derivation function. See the levels 1 and greater in the below figure illustrating the derivation of further canister keys based on the canister root key. This derivation is supported by the ECDSA API through the ecdsa_public_key method, and through the Schnorr API with the schnorr_public_key method.

The derivation of further t-sig keys from a canister root key can be done without involvement of ICP as well to facilitate certain use cases.

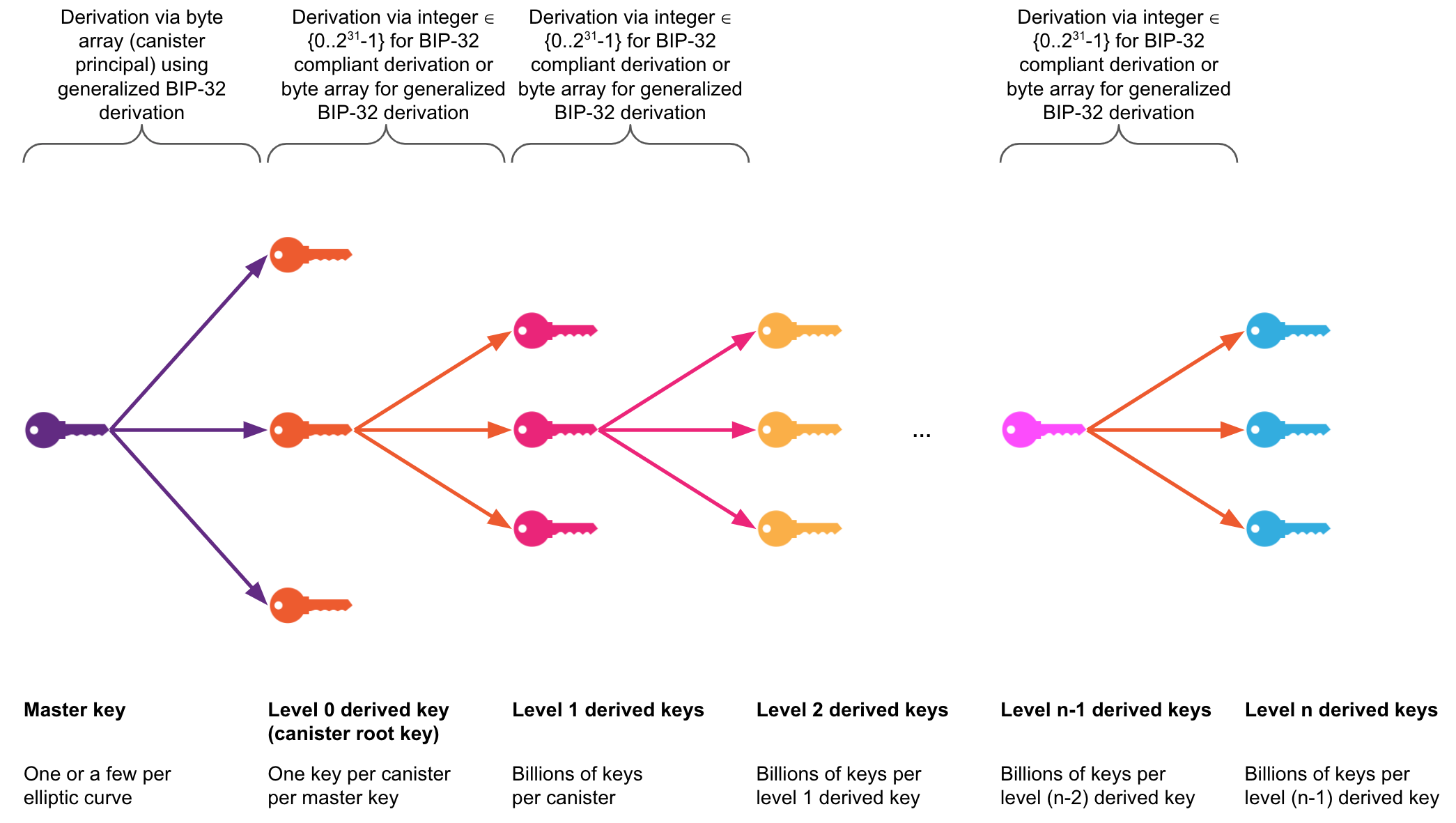
Threshold master keys are always referred to through key identifiers in the t-sig APIs (as well as in the NNS proposals for managing the rollout). The key identifiers comprise an elliptic curve name or an algorithm and an identifier, e.g., an example key identifier is the 2-tuple (secp256k1, test_key_1) for ECDSA or (bip340secp256k1, test_key_1) for Schnorr. Those key identifiers are used by the system to refer to the correct key, e.g., for selecting the key share when computing a signature or in the implementation of the XNet routing of API calls and responses to/from the t-sig-enabled subnet holding the key with the corresponding identifier.

There are currently three master keys deployed, an ECDSA test key, an ECDSA production key, and a Schnorr test key.

• (secp256k1, test_key_1): The ECDSA test key deployed on a single 13-node subnet.
• (secp256k1, key_1): The ECDSA production key deployed on two high-replication subnets, one activated for signing, and the other one for backing up the key for better key availability.
• (bip340secp256k1, test_key_1): The Schnorr test key deployed on a single 13-node subnet.

Deployment

Next, this guide outlines the deployments for the Chromium (Beta) release of the ECDSA test key, the general availability release of the ECDSA production key, and the Deuterium (Beta) release of the Schnorr test key.

Chromium ECDSA release (Beta)

As part of the Chromium release, a test ECDSA key for curve secp256k1 has been deployed on one subnet with a replication factor of 13. This key may be deleted with an according NNS proposal some time after the GA ECDSA release and therefore should not be used for anything that has value, but only for development and testing purposes. More concretely, it is, for example, strongly advised against holding real bitcoin with the test key as those Bitcoin would be lost when the key gets deleted. The test key is rather intended to facilitate development of Bitcoin smart contracts and hold Testnet bitcoin as preparation for the GA ECDSA release. The test key has the id (secp256k1, test_key_1) for referring to it in API calls.

General availability release of ECDSA

A single threshold ECDSA production key for the secp256k1 elliptic curve has been deployed with the GA ECDSA release. The key with id (secp256k1, key_1) will be maintained in secret-shared form on two different subnets with high replication factor (28 nodes initially). The key will be initially generated on a high-replication subnet and kept there and re-shared to a new high-replication subnet using the re-sharing protocol. The latter subnet will be activated to act as the active signing subnet for this key. The further will hold the key in secret-shared form for backup purposes for achieving better key availability, but will not respond to signing requests. In case of the unlikely event of one of the subnets getting destroyed beyond recoverability, the approach of key replication improves key availability by allowing for the key to be re-shared to a different subnet, should this ever be required in case of a disaster.

Deuterium Schnorr release (Beta)

As part of the Deuterium release, a test Schnorr key according to the bip340 specification for curve secp256k1 has been deployed on one subnet with a replication factor of 13. As above, this key may be deleted at some time after the GA Schnorr release and therefore should not be used for anything that has value, but only for development and testing purposes. The test key has the id (bip340secp256k1, test_key_1) for referring to it in API calls.

Further aspects

Support for further elliptic curves and signature schemes may be added in the future. ECDSA signatures over curve secp256r1 and Ed25519 signatures are interesting for supporting use cases such as decentralized certification authorities (CAs) and are the premier candidate group to be added to facilitate use cases like the mentioned one, as well as enabling the direct integration with other blockchains.

Threshold signature APIs

Next, this guide gives an overview of the APIs for threshold signatures. For the authoritative specification, the reader is referred to the corresponding part of the Internet Computer interface specification for ECDSA and Schnorr. The ECDSA API comprises two methods: ecdsa_public_key for retrieving threshold ECDSA public keys, and sign_with_ecdsa for requesting threshold ECDSA signatures to be computed from the subnet holding the secret-shared private threshold ECDSA key. The Schnorr API comprises two methods: schnorr_public_key for retrieving threshold Schnorr public keys, and sign_with_schnorr for requesting threshold Schnorr signatures to be computed from the subnet holding the secret-shared private threshold Schnorr key.

Each API call refers to a t-sig master key by virtue of a 2-part identifier comprising a curve or algorithm, and a key id as outlined above. Derivation paths are used to refer to keys below a canister's root key in the key derivation hierarchy. The key derivation from the master key to the canister root key is implicit in the API.

• ecdsa_public_key: This method returns a SEC1-encoded ECDSA public key for the given canister using the given derivation path.

If the canister_id is unspecified, it will default to the canister id of the caller. The derivation_path is a vector of variable length byte strings. The key_id is a struct specifying both a curve and a name. The availability of a particular key_id depends on implementation.

For curve secp256k1, the public key is derived using a generalization of BIP32 (see ia.cr/2021/1330, Appendix D). To derive (non-hardened) BIP-0032-compatible public keys, each byte string (blob) in the derivation_path must be a 4-byte big-endian encoding of an unsigned integer less than 2³¹. The return result is an extended public key consisting of an ECDSA public_key, encoded in SEC1 compressed form, and a chain_code, which can be used to deterministically derive child keys of the public_key. This call requires that the ECDSA feature is enabled, and the canister_id meets the requirement of a canister id. Otherwise it will be rejected.

• sign_with_ecdsa: this method returns a new ECDSA signature of the given message_hash that can be separately verified against a derived ECDSA public key.

This public key can be obtained by calling ecdsa_public_key with the caller's canister_id, and the same derivation_path and key_id used here.

The signatures are encoded as the concatenation of the SEC1 encodings of the two values r and s. For curve secp256k1, this corresponds to 32-byte big-endian encoding.
This call requires that the ECDSA feature is enabled, the caller is a canister, and message_hash is 32 bytes long. Otherwise it will be rejected.

• schnorr_public_key: Returns a Schnorr public key for the given canister using the given derivation path.

If the canister_id is unspecified, it will default to the canister id of the caller. The derivation_path is a vector of variable length byte strings. The key_id is a struct specifying both a curve and a name. The availability of a particular key_id depends on implementation.

The return value is an extended Schnorr public key consisting of a Schnorr public_key and a chain_code. The chain code can be used to deterministically derive child keys of the public_key. Both the derivation and the encoding of the public key depends on the key ID's algorithm:

For algorithm bip340secp256k1, the public key is derived using the generalization of BIP32 defined in ia.cr/2021/1330, Appendix D. To derive (non-hardened) BIP32-compatible public keys, each byte string (blob) in the derivation_path must be a 4-byte big-endian encoding of an unsigned integer less than 231. If the derivation_path contains a byte string that is not a 4-byte big-endian encoding of an unsigned integer less than 231, then a derived public key will be returned, but that key derivation process will not be compatible with the BIP32 standard. The public key is encoded in SEC1 compressed form. To use BIP32 public keys to verify BIP340 Schnorr signatures, the first byte of the (33-byte) SEC1-encoded public key must be removed (see BIP-340, Public Key Conversion).

This call requires that the Schnorr feature is enabled, and the canister_id meets the requirement of a canister id. Otherwise it will be rejected.

• sign_with_schnorr: Returns a new Schnorr signature of the given message of arbitrary size that can be separately verified against a derived Schnorr public key.

This public key can be obtained by calling schnorr_public_key with the caller's canister_id, and the same derivation_path and key_id used here.

For bip340secp256k1, the signature will be encoded according to BIP340, using 64 bytes. This call requires that the Schnorr feature is enabled and the caller is a canister. Otherwise it will be rejected.

An example of the ECDSA API can be found below:

  ecdsa_public_key : (record {
    canister_id : opt canister_id;
    derivation_path : vec blob;
    key_id : record { curve: ecdsa_curve; name: text };
  }) -> (record { public_key : blob; chain_code : blob; });
  sign_with_ecdsa : (record {
    message_hash : blob;
    derivation_path : vec blob;
    key_id : record { curve: ecdsa_curve; name: text };
  }) -> (record { signature : blob });

An example of the Schnorr API can be found below:

  schnorr_public_key : (record {
    canister_id : opt canister_id;
    derivation_path : vec blob;
    key_id : record { algorithm: schnorr_algorithm; name: text };
  }) -> (record { public_key : blob; chain_code : blob; });
  sign_with_schnorr : (record {
    message : blob;
    derivation_path : vec blob;
    key_id : record { algorithm: schnorr_algorithm; name: text };
  }) -> (record { signature : blob });

Note that in case of high system load, a request to compute a threshold signature may time out. In this case, the canister may want to back off and retry the request later.

API fees

The fees for the t-sig APIs are as defined below. The threshold ECDSA test key and Schnorr test key reside on a regular-sized (13-node) application subnet, while the threshold ECDSA production key resides on a 28-node-sized fiduciary subnet. The subnet size of the subnet where the t-sig key resides and the signatures are computed define the resulting cost. The size of the subnet of the calling canister does not matter for the fees. For costs in USD, the USD/XDR exchange rate as of of November 23, 2022 has been used.

If a canister using this feature is intended to be blackholed, but also for other canisters, it is recommended to send more cycles with the call than the advertised cost of the call so that if the subnet size of the signing subnet increases in the future, the higher costs per signature are still covered. Any cycles not charged in a call are refunded.

Fees for the t-ECDSA test key

Transaction	Description	Cycles (test key)	USD
Threshold ECDSA signing	For computing one threshold ECDSA signature (sign_with_ecdsa)	10_000_000_000	$0.0132551

Fees for the t-ECDSA production key

Transaction	Description	Cycles (production key)	USD
Threshold ECDSA signing	For computing one threshold ECDSA signature (sign_with_ecdsa)	26_153_846_153	$0.0346672

Fees for the t-Schnorr test key

Transaction	Description	Cycles (test key)	USD
Threshold Schnorr signing	For computing one threshold Schnorr signature (sign_with_schnorr)	10_000_000_000	$0.0130886

Environments

In order to facilitate developers throughout the canister development lifecycle on ICP, these features are available in both the SDK for local development and testing as well as on ICP for pre-production testing and production operation of canisters.

SDK

The development of canisters is typically done in the developer's local environment, facilitated by use of the SDK. The SDK has been extended such that the management canister API for threshold ECDSA and threshold Schnorr is available in the local canister execution environment. Thus, canisters using the t-sig APIs can be run locally for development and testing purposes. They are always enabled in the SDK, so no further user action is required in order to make use of the APIs.

When the replica of the SDK environment is first started up, a new t-sig key is generated. This key is then stored in non-volatile memory so that it does not change with every restart of the replica.

For the technically interested readers, it is important to note that the SDK uses the exact same implementations of t-sigs as the mainnet, but only runs a single replica. Thus, the protocol is operating with a single replica, which means it degenerates to a special case and incurs only little overhead, e.g., for key generation and signing, and can thus remain enabled by default in the SDK without noticeably affecting performance of the SDK environment. Also note that the signing throughput and latency in the local SDK environment is not representative for the throughput and latency on ICP.

The Deuterium release is currently only supported in the current beta version of the SDK.

Internet Computer

Any canister on any subnet of ICP can call the t-sig APIs exposed by the management canister. The calls are routed via XNet communication to the t-sig-enabled subnet that holds the keys referred to in the API call (only one such signing subnet holding a test key and one signing subnet holding the production key are available currently). Note that test keys are hosted on a subnet with a replication factor of only 13 and may be deleted in the future, thus they should not be used for anything of value, but rather solely for development and testing purposes. The main intended purpose is to facilitate the development and testing of Bitcoin-enabled dapps using Bitcoin testnet.